Les nombres dans l'audio
Même si nous travaillons avec le son et que nos principaux moyens d'évaluation sont nos oreilles, nous devons parfois utiliser des valeurs numériques pour décrire le son. La plupart des spécifications sont basées sur des chiffres. Lorsque nous enregistrons, nous utilisons des chiffres pour décrire la quantité de données. Si nous voulons communiquer un niveau de pression acoustique, nous utilisons des chiffres. Et cela ne s'arrête pas là.

Décade ou octave
Lorsque l'on décrit la pente d'atténuation, ou de gain, d'un filtre en audio, il est courant de la définir par "dB par octave" comme 6 dB par octave ou, en abrégé, 6 dB/oct.
Cependant, dans d'autres domaines de l'électronique, on décrit la pente par décennie, par exemple 20 dB par décennie.
Une octave est définie comme le doublement ou la division par deux d'une valeur de fréquence. Une décade est définie comme dix fois (ou un dixième) une quantité (ou une gamme de fréquences) ; cela signifie que les valeurs ne sont pas fixes, mais relatives. La gamme de fréquences de l'oreille humaine est d'environ dix octaves ou trois décades, de 20 Hz à 20 000 Hz.
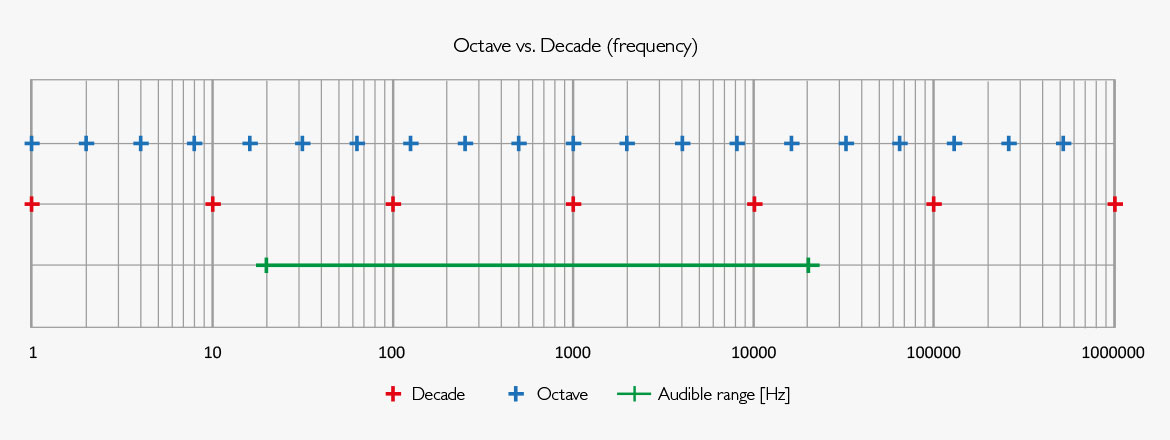
Fig 1 Série de chiffres indiqués par des intervalles d'octave et de décade.
L'ordre d'un filtre définit la pente en dehors de sa bande passante. Un filtre du premier ordre contient, en principe, un composant électronique dont la résistance dépend de la fréquence. Ce composant est généralement une bobine ou un condensateur en liaison avec une résistance. La pente est de ±6 dB par octave selon la configuration des deux composants. Un filtre du second ordre comprend deux de ces composants en combinaison avec une résistance, comme deux condensateurs ou une bobine et un condensateur : La pente obtenue est alors de ±12 dB par octave. Aujourd'hui, ces filtres ne se trouvent généralement que dans les haut-parleurs passifs, mais la plupart des filtres sont réalisés numériquement via un DSP.
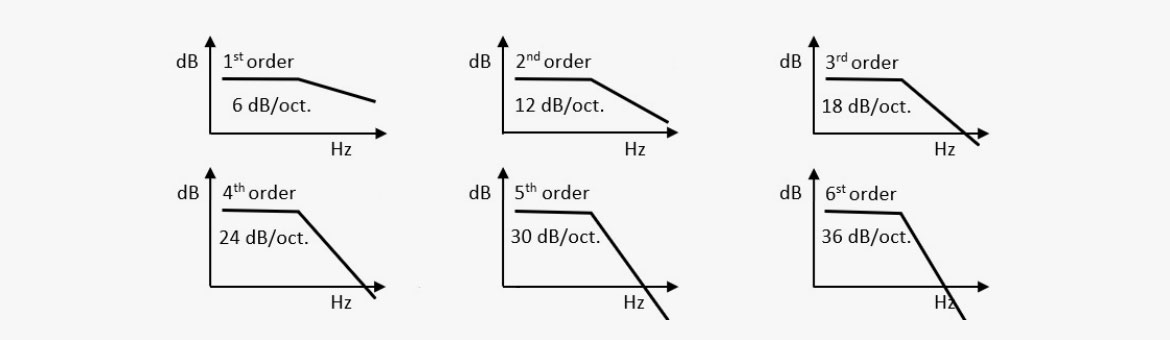
Le tableau ci-dessous indique l'ordre des filtres et les pentes afférentes (ici l'atténuation) définies en dB/oct ou dB/décade.
| Ordres des filtres | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| dB/octave | 3 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| dB/decade | 10 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
Table de conversion : Pentes de filtre définies par l'ordre du filtre, dB/oct ou dB/décade.
Échelles linéaires et logarithmiques
Il existe un intervalle fixe entre chaque unité de l'échelle linéaire (par exemple, 1, 2, 3, 4, où la distance entre chaque unité est de 1).
L'échelle logarithmique a un rapport fixe entre chaque unité de l'échelle (par exemple, rapport 10, les unités sont : 1-10-100-1000, etc. - ou rapport 2, les unités sont : 1-2-4-8-16, etc.) Cette échelle logarithmique s'applique à de nombreuses mesures électriques ou acoustiques, qui concernent les microphones (par exemple, Volt, Pascal, etc.).
Les humains perçoivent à la fois le niveau et la fréquence de manière logarithmique. En ce qui concerne la fréquence, nous interprétons la courbe de réponse en fréquence à l'aide d'une échelle logarithmique. L'échelle des décibels est liée à la façon dont les humains perçoivent le niveau. Ainsi, l'échelle est logarithmique, ce qui donne la perception d'une progression uniforme.
Le décibel (dB)
L'avantage de cette échelle est que 1 dB est à peu près le changement de niveau mineur que vous pouvez entendre. 3 dB est un changement audible évident. 10 dB est subjectivement perçu comme un doublement ou une réduction de moitié. Dans l'ensemble, chaque étape de l'échelle est perçue comme étant de taille égale. Le nombre de dB le plus significatif que vous trouverez dans la vie réelle est <200 dB, c'est-à-dire si le nombre de dB comporte trois chiffres, le premier étant toujours "1".
L'échelle des dB est relative. Ainsi, vous pouvez exprimer tout changement en dB. Un changement de 0 dB correspond à une absence totale de changement. Tout nombre de dB positif indique un changement positif (la valeur est plus élevée qu'avant). Un nombre de dB négatif indique un changement négatif (la valeur est plus basse qu'avant).
Vous pouvez faire du dB une échelle absolue en appliquant une référence - par exemple, le niveau de pression acoustique, la référence étant 20 μPa. Or 0 dB signifie que la pression acoustique est présente, et qu'elle est de 20 μPa (approximativement le seuil d'audition aux fréquences moyennes). Décrivant le niveau de pression acoustique, "dB re 20 μPa" peut également s'écrire "dB SPL" (Sound Pressure Level).
Pour les mesures électriques, une autre référence est 1 Volt, écrite comme "0 dBV" ou "0 dB re 1 Volt". Cette valeur absolue s'applique, par exemple, à la spécification de la sensibilité des microphones.
Largeur de bande, pourcentage et facteur Q
Les égaliseurs paramétriques incluent généralement des réponses de filtre en forme de cloche, des filtres passe-bande. Les paramètres de contrôle fournis sont la fréquence, le niveau et le facteur Q ou la bande passante. Dans les filtres définis pour les techniques de mesure, un pourcentage peut également s'appliquer pour décrire la bande passante. La largeur de bande, le facteur Q et le pourcentage expriment la même chose. Cependant, les paramètres qui s'appliquent dépendent de la marque, du modèle et de l'application du filtre. Sur certains appareils cependant, vous pouvez passer de l'un à l'autre.
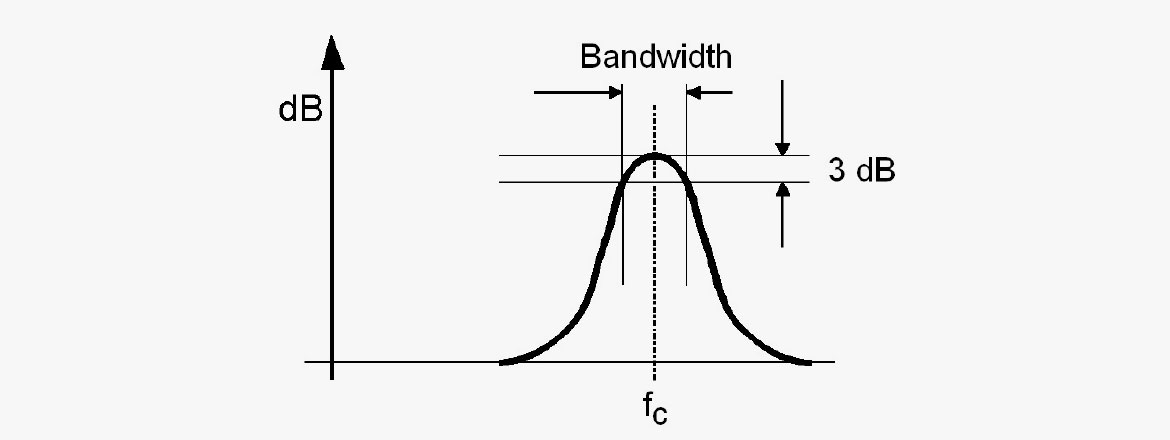
Voici les relations entre les différents termes :
Bande passante
La bande passante est la plage de fréquences entre les points de coupure à -3 dB sur une courbe de réponse, c'est-à-dire f haute - f basse [Hz]. La largeur de bande est exprimée en valeur absolue [Hz] ou relative en octaves (souvent en 1/1 octave, 1/3 octave ou fractions d'octave exprimées par des nombres décimaux, par exemple 0,1 octave).
Pourcentage
La bande passante exprimée en pourcentage :
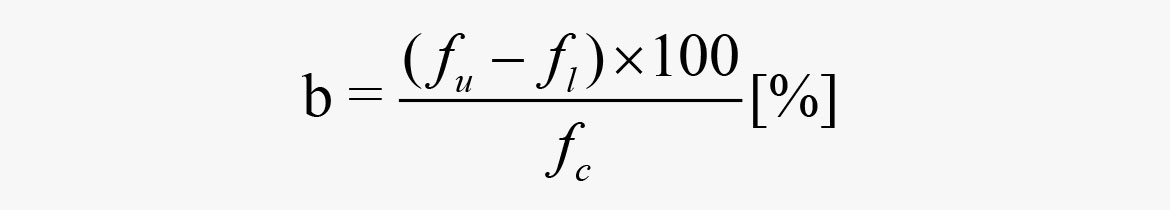
where
fu = fréquence de coupure supérieure [Hz]
fl = seuil de coupure inférieur
fc = fréquence centrale [Hz]
Exemple: (1/1 octave ~ 70%, 1/3 octave ~ 22%).
Facteur Q
Le facteur Q d'un filtre se calcule comme ceci :
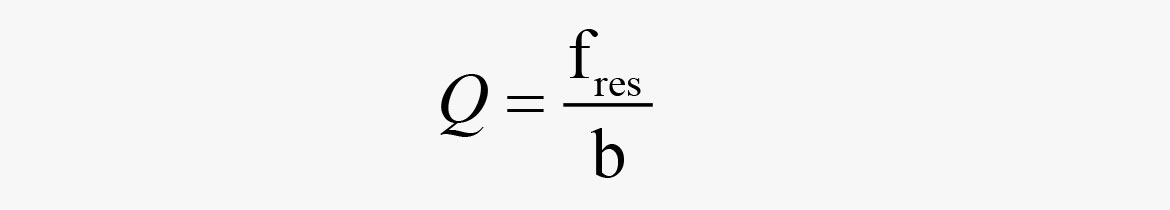
fres = fréquence de résonance/centre [Hz]
b = Largeur de bande [Hz]
Préfixe
Un préfixe est un affixe placé devant un mot ou un nombre pour en modifier le sens. Un préfixe numérique est pratique car il facilite la compréhension des nombres extrêmement petits - ou extrêmement grands.
Un préfixe remplace la notation de la puissance. Par exemple, "2000" équivaut à "2 fois 10 à la puissance 3" ou s'écrit "2*103". Noté par un préfixe : "2k" car "k" indique un facteur de 1000.
Voici une liste des préfixes des numéraux tels que définis par le système SI :
| Prefix | Abbreviation | Power | Value |
| Tera | T | 1012 | 1 000 000 000 000 |
| Giga | G | 109 | 1 000 000 000 |
| Mega | M | 106 | 1 000 000 |
| kilo | k | 103 | 1 000 |
| hecto | h | 102 | 100 |
| deka | da | 101 | 10 |
| base unit | - | 1 | 1 |
| deci | d | 10-1 | 0.1 |
| centi | c | 10-2 | 0.01 |
| milli | m | 10-3 | 0.001 |
| micro | µ | 10-6 | 0.000 001 |
| nano | n | 10-9 | 0.000 000 001 |
| pico | p | 10-12 | 0.000 000 000 001 |
L'unité pour la capacité d'un condensateur est le Farad. Cependant, les condensateurs physiques présentent souvent des valeurs qui sont une petite fraction de l'unité de base ; par exemple, 0,0000000000022 Farad. Il est plus facile de l'écrire sous la forme 2,2 pF (pico Farad).
Ou une résistance peut avoir une valeur de "1000000 Ω, plus facilement notée comme "1 MΩ".
Ou encore, un microphone a une sensibilité de 0,01 V, plus facilement notée comme "10 mV".
Lorsque l'on parle de la pression barométrique de l'air, on se situe aux alentours de 1000 hPa (hecto Pascal). et non 100 kPa, ce qui serait plus simple. Cependant, ici, l'ancienne tradition d'utiliser le Bar au lieu du Pascal transparaît car 1000 milliBar = 1000 hPa.
Confusion entre la numérotation générale et la quantification des données informatiques
Lorsque l'on calcule la taille de toute information numérique traitée par les ordinateurs, il faut savoir que tout est basé sur des octets [B], qui contiennent chacun 8 bits. Ainsi, le nombre de bits par échantillon est calculé comme un nombre entier multiplié par le nombre 8 (1 ' 8, 2 ' 8, 3 ' 8, etc.). Le nombre de bits par échantillon du PCM linéaire est de 8 (1 octet), 16 (2 octets), 24 (3 octets) ou 32 (4 octets). Pour une résolution plus élevée et un traitement interne, 64 bits ou plus peuvent être utilisés.
Comme ces nombres deviennent grands, l'utilisation de préfixes est utile. Les unités de préfixe sont définies dans le système SI, qui utilise "k" (kilo), "M" (Mega), "G" (Giga), "T" (Tera), et ainsi de suite. Cependant, tout en utilisant les mêmes noms de préfixes, c'est la définition binaire que nous appliquons dès que nous décrivons les tailles de fichiers, ce qui est plutôt déroutant !
Voici comment calculer la taille des fichiers tels qu'ils apparaissent sur votre ordinateur :
1 B = 8 bits
1 kB = 1024 B = 8192 bits
1 MB = 1024 kB = 8,388,608 bits (≈ 8.39 ´ 106 bits)
1 GB = 1024 MB ≈ 8.59 ´ 109 bits
1 TB = 1024 GB ≈ 8.8 ´ 1012 bits
Exemple :
Quelle est la capacité de stockage nécessaire pour un enregistrement stéréo d'une heure en 44,1 kHz/16 bits ?
Le nombre total de bits se calcule comme suit :
Fréquence d'échantillonnage x nombre de bits par échantillon ' nombre de canaux audio ' durée de l'enregistrement (en secondes) :
[1 heure = (60 min. ' 60 secondes) = 3600 secondes]
44 100 (échantillons par seconde) ' 16 (bits par échantillon) ' 2 (canaux) ' 3600 (secondes) = 5,08 109 bits
Nombre d'octets : 5.08 ' 109 / 8 = 6.35 ' 108 B
Nombre de kB : 6,35 ' 108 / 1024 = 6,20 ' 105 kB
Nombre de Mo : 6,20 ' 105 / 1024 = 605,6 Mo
Les préfixes pour les nombres à base binaire existent depuis de nombreuses années. Certains fabricants utilisent des préfixes binaires lorsqu'ils spécifient leurs disques durs. Voici un tableau qui compare les préfixes décimaux aux préfixes binaires, tels que définis par la CEI (Commission électrotechnique internationale) ou le JEDEC (Joint Electron Device Engineering Council).
| Décimal | Binaire | ||||||||
| Valeur | SI | Valeur | IEC | JEDEC | |||||
| facteur | symbole | nom | facteur | symbole | nom | symbole | nom | ||
| 1000 | 103 | k | kilo | 1024 | 210 | Ki | kibi | K | kilo |
| 10002 | 106 | M | mega | 10242 | 220 | Mi | mebi | M | mega |
| 10003 | 109 | G | giga | 10243 | 230 | Gi | gibi | G | giga |
| 10004 | 1012 | T | tera | 10244 | 240 | Ti | tebi | - | - |
| 10005 | 1015 | P | peta | 10245 | 250 | Pi | pebi | - | - |
| 10006 | 1018 | E | exa | 10246 | 260 | Ei | exbi | - | - |
| 10007 | 1021 | Z | zetta | 10247 | 270 | Zi | zebi | - | - |
| 10008 | 1024 | Y | yotta | 10248 | 280 | Yi | yobi | - | - |
Tableau Dans ce tableau, les préfixes à base décimale sont comparés aux préfixes à base binaire.
Malheureusement, il est plus courant d'utiliser les préfixes décimaux comme s'ils étaient binaires.
Dans l'exemple mentionné ci-dessus, le calcul correct donne ce résultat : 605,6 Mio.
Notez également que le Ki utilise la lettre majuscule K. Parfois, vous pouvez voir K (sans le "i") signifiant également Ki.
CEI 60027-2, deuxième édition, 2000-11 : Symboles littéraux à utiliser en électrotechnique - Partie 2 : Télécommunications et électronique.


