Von A nach D und zurück - Erläuterung der digitalen Wandlung

Wandlung von Audio

Bei der Wandlung eines analogen Audiosignals in ein digitales Pendant geht es darum, eine kontinuierliche Wellenform in diskrete Zahlen umzusetzen. Bei der späteren Rekonstruktion des Signals verwenden wir diese Zahlen, um das Ursprungssignal Schritt für Schritt wieder zurückzugewinnen.

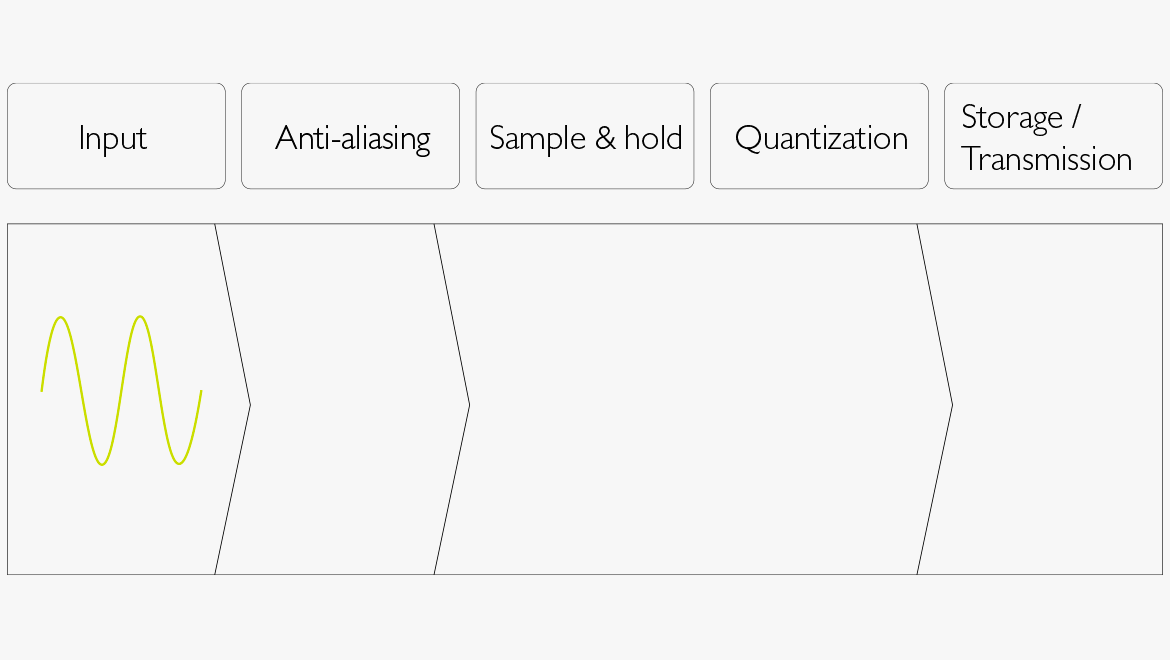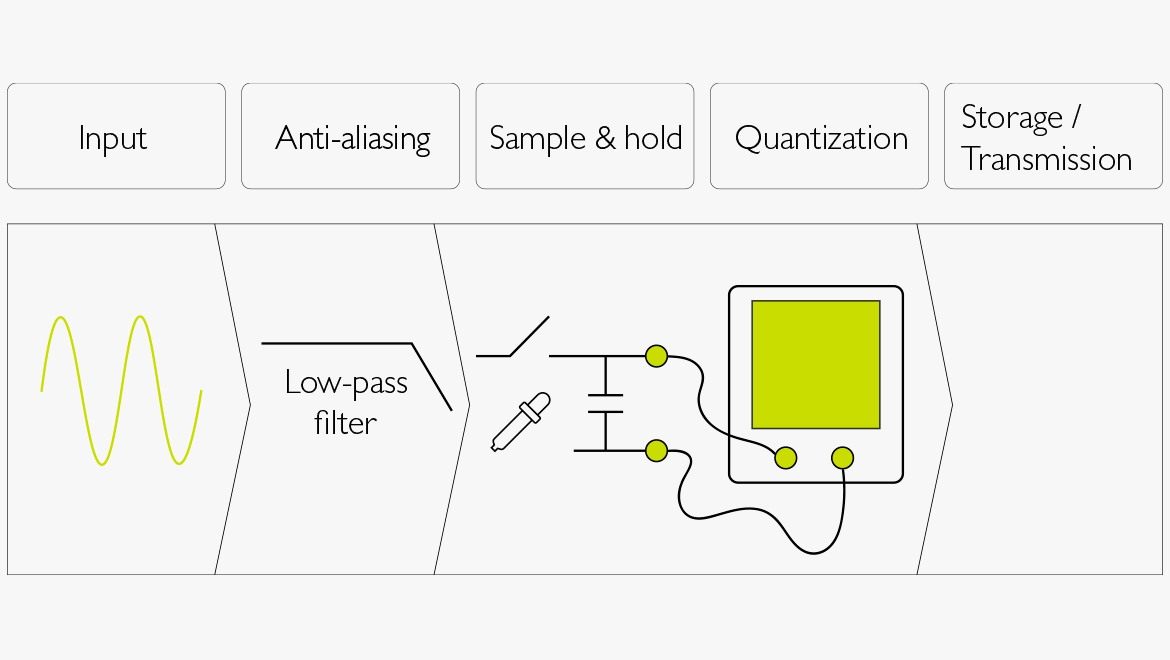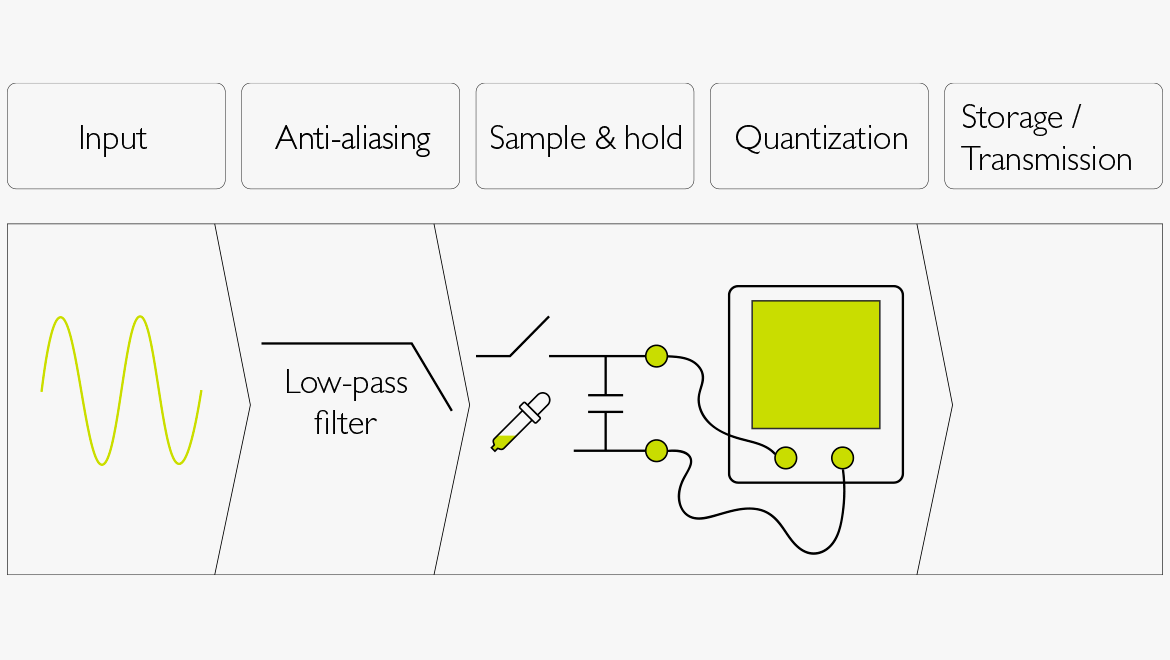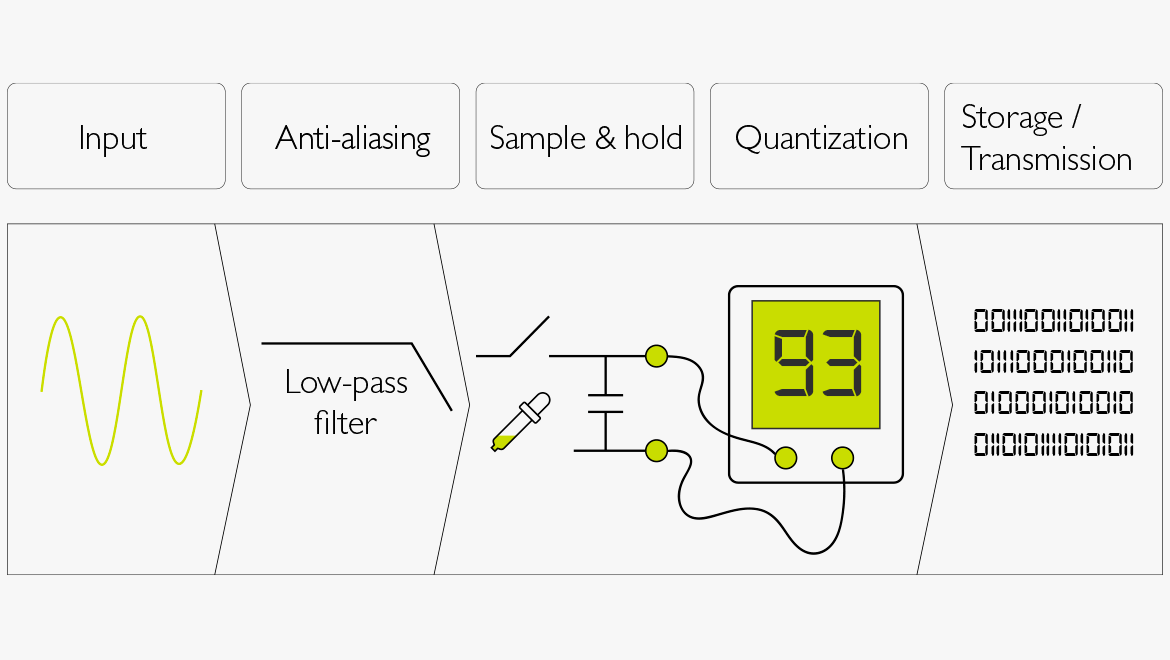
Abbildung 1. Verfahren der Digitalisierungsprozesses von analogem Audio:

1. Der Eingang einer analogen Quelle, bspw. ein Mikrofon.
2. Das Signal wird vor dem Sampling-Vorgang Tiefpass-gefiltert (Anti-Aliasing).
3. Das Sampling (S / H = Sample & Hold) wird bei einer bestimmten Abtastfrequenz durchgeführt, die die obere Grenze für den Frequenzbereich des digitalisierten Audiosignals festlegt.
4. Dabei wird der Wert jedes Samples bestimmt (Quantisierung). Die Anzahl an Bits für jedes Sample legt die Genauigkeit des quantisierten Audiosamples fest. Mehr Bits entsprechen einem größeren Dynamikumfang.
5. Der Binärcode (0en und 1en) wird entweder gespeichert oder an einen anderen Teil der Kette weitergereicht (Speicherung / Übertragung).

Sampling

Die Grundlage der Wandlung basiert auf Samples. Ein Sample ist eine diskrete Messung an einer einzelnen Stelle der Wellenform zu einem bestimmten Zeitpunkt. Unser Sample hat einen einzigen Wert. Dieser kann gespeichert oder an ein anderes Gerät weitergegeben werden.

Ein Sample ist jedoch nicht genug, um einen lebendigen Klang wieder herzustellen. Um in Bezug auf die Wellenform des Audiosignals genügend Informationen zu speichern, bedarf es einer großen Menge an Samples.

Also muss kurz nach der Ermittlung des ersten Samples ein weiteres erfasst werden. Das Signal hat sich weiter entwickelt, also könnte das neue Sample einen neuen Wert haben. Und wieder wird nach dem zweiten Sample ein weiteres ermittelt. Und noch eins. Und so weiter...

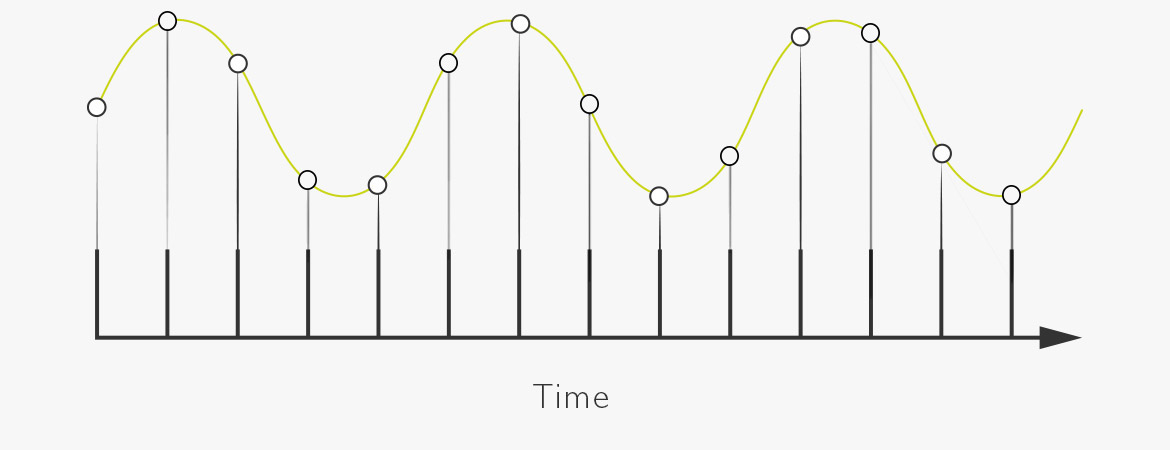
Abbildung 2. Ein Sample wird ermittelt an einem Punkt des ursprünglichen Audio-Signals.

Die Anzahl der Samples, die pro Sekunde ermittelt werden - die Samplingfrequenz - bestimmt die höchste Audiofrequenz, die nach der Digitalisierung rekonstruiert werden kann. Die Regel lautet: Man benötigt mindestens die doppelte Samplingfrequenz im Vergleich zur höchsten Frequenz, die reproduziert werden soll (oder anders ausgedrückt: Man benötigt mindestens zwei Samples für eine Schwingungsperiode des Tonsignals). Wenn Du bis zu 20.000 Hz (20 kHz) aufnehmen möchtest, benötigst Du also mindestens 40.000 Samples pro Sekunde (oder eine Abtastfrequenz von mindestens 40 kHz). Um dies praktikabel umzusetzen, werden für diese Anwendung standardisierte Abtastfrequenzen verwendet, wie 44.100 Hz und 48.000 Hz.

Aliasing

Wenn Du die Regel von mindestens zwei Samples pro Schwingungsperiode des Audiosignals missachtest, können unerwünschte Aliasing-Frequenzen erfasst werden. Aliasing steht für einen Identitätswechsel (wie bei James Bond / 007). Um das zu verhindern, muss vor dem Sampling ein "Anti-Alias"-Filter eingesetzt werden. Dies ist ein Low-Pass-Filter, der Frequenzen abschneidet, die über der halben Abtastrate liegen.

Diese Art Filter kann das Audiosignal beeinflussen. Oversampling (eine Überabtastung, bspw. durch Verdopplung oder Vervierfachung der Abtastfrequenz) wird verwendet, um den Einfluss des Filters zu reduzieren. (Eine Verdopplung der Abtastfrequenz bedeutet allerdings auch eine Verdopplung der entstehenden Daten für eine Aufnahme.)

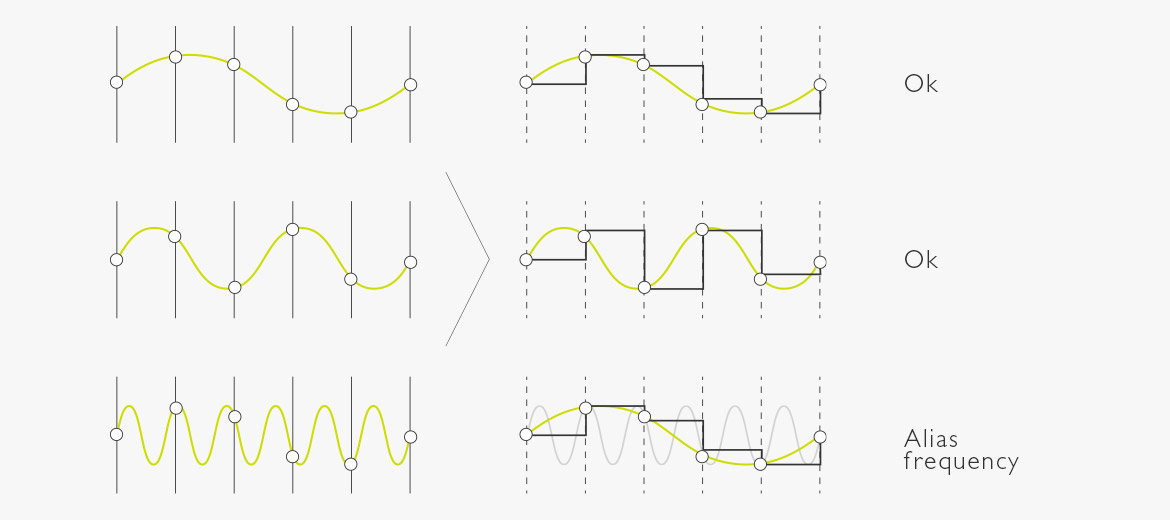
Abbildung 3. Abtastfrequenz

Wenn die Abtastfrequenz nicht mindestens dem Doppelten der höchsten Audiofrequenz entspricht, entspricht das rekonstruierte Signal nicht dem Eingangssignal.

Oben: Die eine Schwingung des Signals wird sechs Mal abgetastet / gesampelt. 6 > 2, also ist die Rekonstruktion okay.
Mitte: Die beiden Schwingungen des Signals werden sechs Mal abgetastet / gesampelt, was drei Abtastungen je Periode entspricht. 3 > 2, also ist die Rekonstruktion okay.

Unten: Die sechs Schwingungen des Signals werden sechs Mal abgetastet / gesampelt, was einer Abtastung je Schwingung entspricht. 1 < 2, also endet das Signal als Alias-Frequenz, die vom Original abweicht.

Jitter

Ein anderer sehr wichtiger Aspekt während einer Wandlung ist der Intervall zwischen den Samples. Jedes Intervall muss exakt die gleiche Länge haben, denn nach der Digitalisierung liegen keine Information über den Zeitpunkt eines Samples vor. Daher müssen wir uns auf eine stetige Wiederholung der Abtastung verlassen - ein konstantes Intervall. (Bei einer Samplingfrequeng von 48 kHz beträgt das Intervall zwischen zwei Samples 20.833 Mikrosekunden [µs].)

Der Abtast-Takt muss stabil sein und sollte durch nichts gestört werden. (Nicht-Exakte Abtastwiederholung, auch Jitter genannt, führt zu Rauschen im reproduzierten Audio-Signal.)

Quantisierung

Wie zuvor bemerkt, bildet jedes Sample eine Stelle im Original-Signal ab. Es ist wichtig, dass die Messung jedes Punkts und die gespeicherten Werte so genau wie möglich sind. Nach dem Abtastvorgang ist jede Referenz zum Originalsignal verloren.

Das Festlegen eines Werts zum Abtastzeitpunkt entspricht der Verwendung eines Maßbands in einer Werkstatt. Wenn Du einen Regalboden für Deinen Schrank aussägen möchtest, musst Du ihn ausmessen um zu ermitteln, wie groß er sein muss. Wenn Dein Maßband jetzt nur Meter oder Yards anzeigt, ist es nahezu unmöglich, die richtige Größe zu ermitteln. Wenn das Maßband auch Zentimeter oder Zoll anzeigt, wird die Genauigkeit schon besser. Der Boden mag aber immer noch nicht genau in den Schrank passen. Wenn das Maßband auch Millimeter oder Anteile von Zoll anzeigt, ist die Genauigkeit hoch genug, um die Größe zu beschreiben.

Der Begriff Quantisierung kommt vom lateinischen Wort 'quantitas', was Menge oder Größe bedeutet. Um die Größe eines Samples zu beschreiben, verwenden wir Bit. 'Bit' ist eine Zusammensetzung aus den Worten 'binary digit' (Binärziffer). Binär (Binary) bedeutet, die Ziffer kann nur einen von zwei Werten haben, 0 oder 1. Wenn wir größere Zahlen abbilden möchten, müssen wir mehr Bits verwenden. Beispielsweise erlaubt uns die Verwendung von zwei Ziffern die Abbildung von vier Werten: 00, 01, 10 und 11. Durch Hinzufügen weiterer Bits wird der Wertebereich durch jedes weitere Bit verdoppelt.

Die Genauigkeit der Messung - oder Quantisierung - wird durch die Menge an verfügbaren Bits für jedes Sample festgelegt. Jeder Bitwert repräsentiert einen vordefinierten Wert. Wenn der Originalwert genau einem der vordefinierten Werte entspricht, ist alles in Ordnung. Wenn dies nicht der Fall ist, musst Du den bestpassenden Wert hinnehmen. Das bringt allerdings einen Fehler mit sich, der nicht wieder kompensiert werden kann. Um also Fehler zu reduzieren ist es wichtig, eine hinreichende Zahl an Bits pro Sample zur Verfügung zu stellen. Wenige Bits pro Sample verursachen Verzerrung. Eine Erhöhung der Bits ändert die wahrgenommene Verzerrung in ein Rauschen. Dann bleibt die Frage, wie rauscharm Deine Wandlung sein soll. Generell verbessert sich das S/N-Verhältnis um 6 dB für jedes zusätzliche Bit.

Computer organisieren Bits in Gruppen zu 8, die bevorzugte (praktische) Anzahl an Bits pro Sample ist also 8, 16, 24, etc. 8 Bit pro Sample ist zu gering für einen hochwertigen Klang. Ein 16-Bit-Sample entspricht Klang in CD-Qualität. Für die Produktion von qualitativ hochwertigem Ton werden 24-Bit-Samples genutzt.

Abbildung 4. Quantisierung
Mit der Quantisierung bestimmt die Zahl der Bits die Genauigkeit des gelesenen Werts. Jedes Mal, wenn ein weiteres Bit zur Verfügung steht, verdoppelt sich die Auflösung der Skala und die Messfehler werden halbiert. In der Praxis bedeutet dies, dass das S/N-Verhältnis sich für jedes zusätzliche Bit um etwa 6 dB verbessert.

D-A

Bei der Wandlung von digital nach analog besteht die Aufgabe darin, ein Signal zu generieren, das proportional zu den Bitwerten ist, die in den digitalen Informationen enthalten sind. Jedes Bit repräsentiert dabei einen Spannungswert. Das wichtigste Bit (MSB) wandelt sich in die größte Spannung, das nächst signifikante Bit in die Hälfte dessen und so weiter, bis hin zum wenigsten signifikanten Bit (LSB). Durch die Addition aller Spannungsstufen und durch Aufrechterhaltung der aufsummierten Spannung bis zur Aktivierung des nächsten Samples wird ein kontinuierlicher Spannungsverlauf erzeugt. Das Signal wird dann wieder über einen Low-Pass-Filter geglättet.

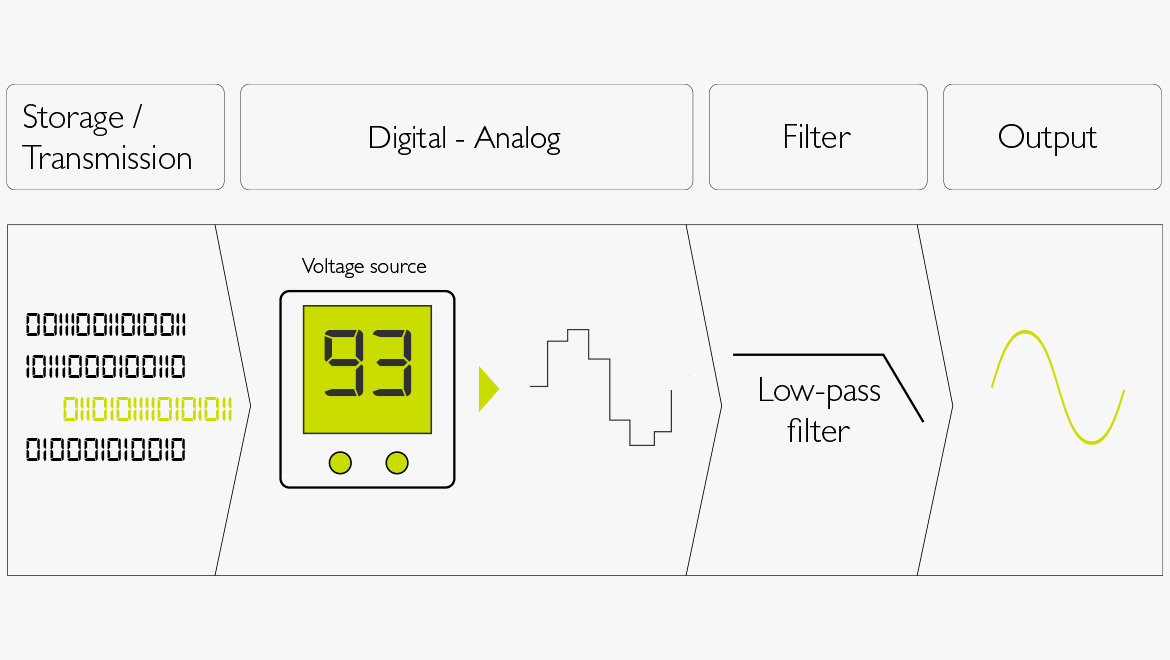
Abbildung 5. D/A-Wandlung

1. Bei der Digital-Analog-Wandlung werden die gespeicherten Zahlen zurück in analoge Werte konvertiert.
2. Die Zahlen werden in ein programmierbares Netzteil eingelesen, sodass sie entsprechende Spannungsstufen generieren können.
3. Der Low-Pass-Filter glättet das Signal durch Entfernen der harmonischen Obertöne (die durch diese Stufen erzeugt werden), die oberhalb dieses Frequenzspektrums liegen.
4. Der Ausgang ist rein analoges Audio.